1 Answers

编辑器默认的负数护甲公式存在设计问题

之前论坛上的一个解决方案其实也不合理
https://create-bbs.reckfeng.com/forum.php?mod=viewthread&tid=1127
这个方案是把下图红框-号改成+号
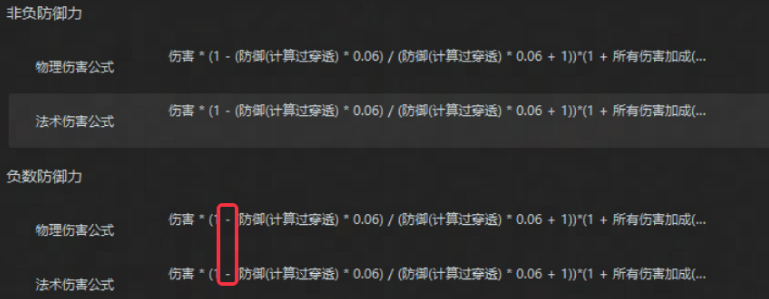
image.png
这个方案一定程度上能缓解，但不能根治。

原因简析

设 x = 防御（计算过穿透）
原始伤害公式 = 伤害*(1-0.06x/(0.06x+1))
设y = 0.06x/(0.06x+1)
那么y在正数护甲时，y可以理解为减伤%，而在负数护甲时，y应该理解为增伤%
为了方便理解，下面直接看y= 1-0.06x/(0.06x+1)的函数曲线，可以看到它是一个反比例函数
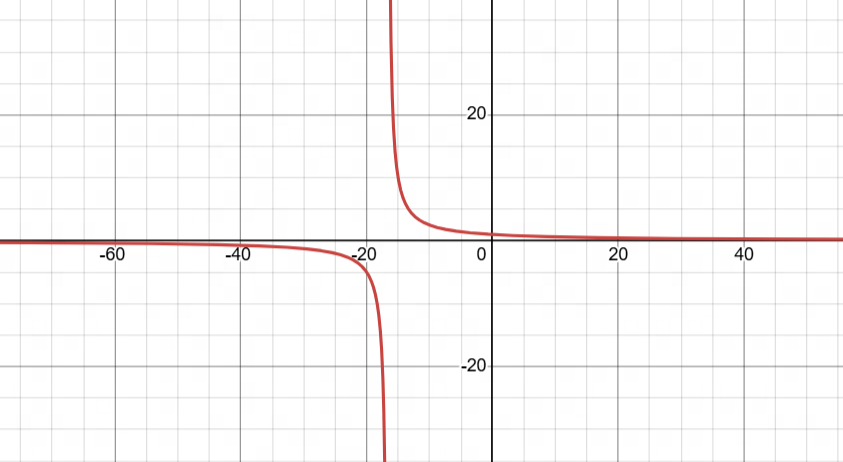
image.png
当定义域为[0,+∞)时，它的值域是[0,1)，并且可以看出护甲越高时，伤害越低，同时继续堆护甲的收益会越来越低，这是符合期望的
但是当x<0时，会存在一个阈值，也就是0.06x+1 = 0，也就是x≈-16.67时（反比例函数的特性，分母无法为0）。
当-16.67<x<0时，伤害会乘上一个大于1的数，看上去是增伤了，其实这时的伤害公式也还是不合理的，比如当护甲非常接近-16.67时，伤害会获得巨大的增伤。而超过-16.67时，反而可能回血，这显然是不合理的。
即便改为y=1+0.06x/(0.06x+1)，也无法解决负数伤害的问题，下图为y=1+0.06x/(0.06x+1)的函数图
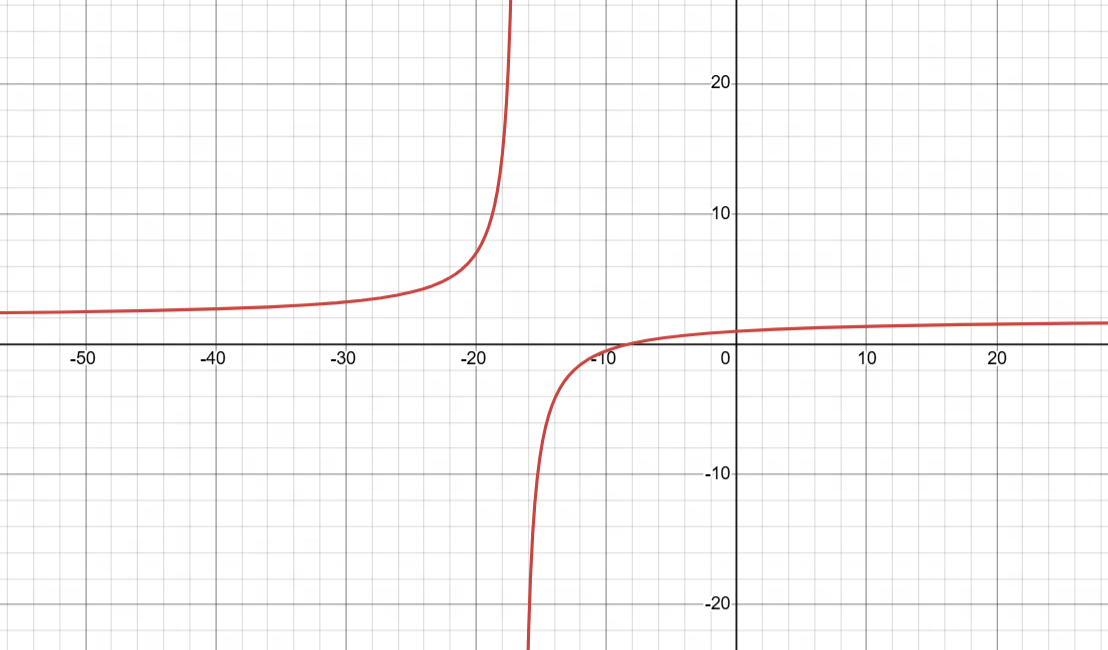
image.png

推荐的解决方案(参照War3伤害公式)

  1. 把负数护甲公式里护甲相关的乘区删掉，改为全局事件中实现（因为涉及指数运算，公式里不支持）
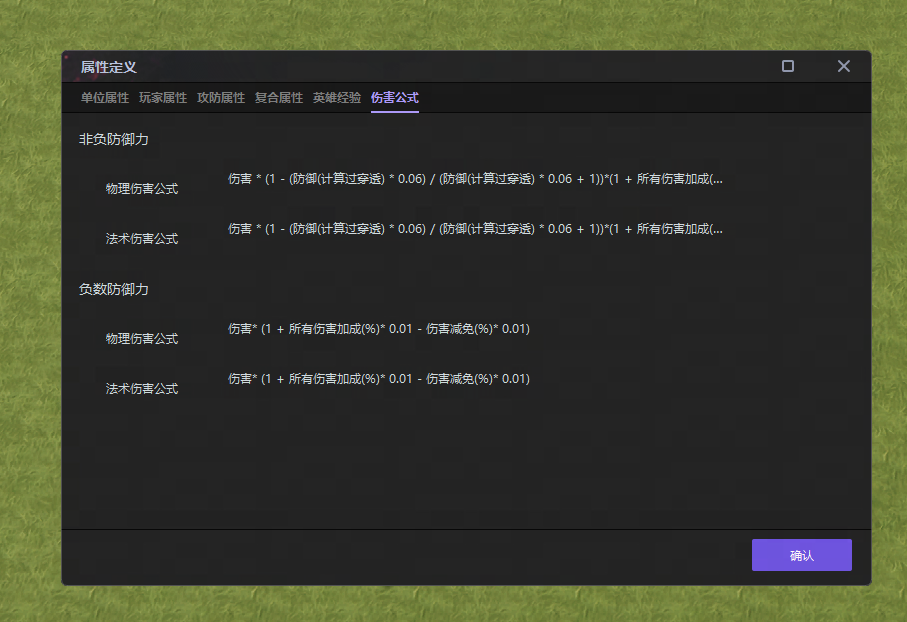
    f7080f7db05de618df9fcb8aae33f6f3.png
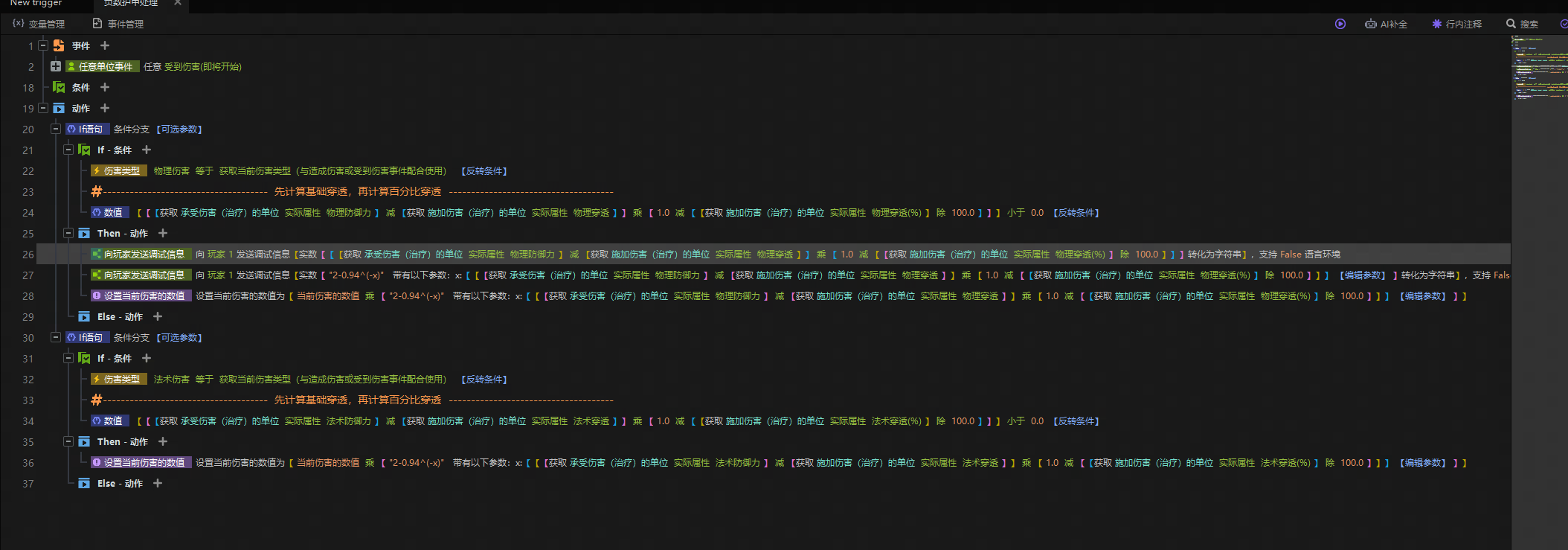
  2. 全局伤害事件中实现负数伤害增伤
    更改后的负护甲伤害公式 = 伤害*(2-0.94^(-护甲值))×伤害加成×伤害减免
    70a1b3881c0519eec436c121c2104e83.png
BAIMO1
Related